【学习笔记】元学习(Meta Learning)学习笔记
致谢李宏毅老师的视频教程:https://www.bilibili.com/video/av46561029/?p=32
前言
· 为何要研究Meta Learning?
尽管我是研究生成模型的,但是最近对于meta learning产生了强烈的兴趣。理由在于,GANs本身是一个特别吃数据集的模型,从某种意义上来说,数据集的好坏对最后生成效果的影响,不亚于甚至高于生成模型本身的设计对最后生成效果的影响。造成这一现象的原因是,GANs学习的本质是拟合数据的潜分布,而数据潜分布很大程度上由训练数据所具有的样本广度和质量来决定,因此GANs的训练效果容易受到来自训练数据的质量的影响。
如何摆脱这种GANs对于数据集的过度依赖呢?一个比较好的检测方法是在少样本学习(few-shot learning)上检验模型的学习效果。但是直接用GANs架构是很难实现少样本学习的,原因是在数据量大的时候,充足的训练样本能够让判别器精准地找到真假样本的划分界线,从而让生成器拟合出精确的生成分布,但是在数据量少的时候,要想准确地拟合数据的潜分布就会变得比较困难。
最近出现的meta learning为解决这一问题提供了比较好的方法,首先因为meta learning已经被证明在少样本学习上取得了较好的效果,另外meta learning的方法也比较符合GANs的学习需求。为何这么说呢?meta learning的目标是学习如何去学习,换言之,它能够依靠对数据集规律的探索去制定学习策略,从而将传统GANs的训练过程由设计模型->寻找数据->验证模型,变为寻找数据->设计模型->验证模型,这对于我们解决GANs训练中的数据不匹配以及数据缺乏问题带来很大的帮助。
综上,meta learning将GANs的传统训练思维,由用数据去匹配模型,转变为用模型去匹配数据,为解决生成模型的少样本学习问题提供了突破口。下面是meta learning学习笔记的正文。
第一章 Meta Learning概述
Meta Learning被称作元学习,不同于Machine Learning的目标是让机器能够学习,Meta Learning则是要让机器学会如何去学习。
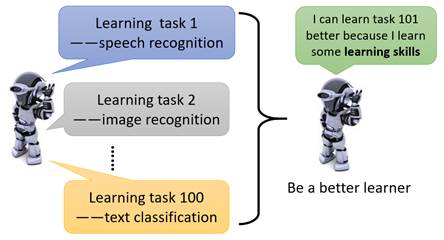
举例来说,机器已经在过去的100个任务上进行了学习,现在我们希望,机器能够基于过去100个任务学习的经验,变成一个更厉害的学习者,这样当在第101个新任务到来之时,机器能够更快地学习。值得注意的是,机器之所以能够学习地更快并不是依赖于在旧任务中已获取的“知识”,而是机器学到了如何去更好获取知识的方法,并将这一方法应用于新任务当中,从而较快地提升学习效率。
以上图为例,假设前99个学习任务都是各种辨识任务,例如语音辨识、图像辨识等,在前99个任务学习完成之后,我们给机器一个新的学习任务,而这个新的学习任务与前99个任务没有任何关联,譬如是一个文本分类任务。而现在,Meta Learning的目的就是希望能够通过前99个辨识任务的学习让机器在新的文本分类任务上学习得更好,也就是说,机器在前面的学习中不仅仅学到了如何解决某些特定的任务,而是学习到了学习本身这件事情,从而能提升自己在面对新任务上的学习能力。所以,Meta Learning就是一门研究如何让机器学会更好地学习的新兴研究方向。
第二章 Meta Learning的建模思路
前篇提及的概念描述可能依然比较抽象,下面我们用具体的模型架构来解释一下Meta Learning实际上在做的事情。
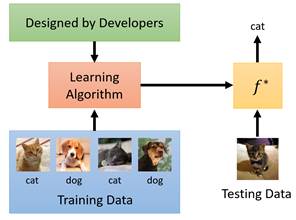
首先,上图描述的是传统机器学习在做的事情——由人来设计一套学习算法,然后这个算法会输入一堆训练资料,通过长时间的训练得到算法里的参数,这堆参数拟合出一个函数![]() ,然后用测试资料来测试这个
,然后用测试资料来测试这个![]() ,如果效果达标就证明机器学到了该特定任务的实现函数
,如果效果达标就证明机器学到了该特定任务的实现函数![]() 。而Meta Learning做的事情与上述描述不同的地方在于,将其中由人来设计学习方法的过程,改成了由机器来设计一套学习方法。
。而Meta Learning做的事情与上述描述不同的地方在于,将其中由人来设计学习方法的过程,改成了由机器来设计一套学习方法。

如上图所示,如果将原本机器学习中的训练资料记为![]() ,那么在Meta Learning中的训练资料变为一堆
,那么在Meta Learning中的训练资料变为一堆![]() 和一堆
和一堆![]() 的组合,然后现在机器要求解的结果不再是
的组合,然后现在机器要求解的结果不再是![]() ,而是一个新的函数
,而是一个新的函数![]() ,这个
,这个![]() 决定在给定
决定在给定![]() 的情况下
的情况下![]() 的结果。
的结果。
简言之,如果机器学习的定义表述为:根据资料找一个函数f的能力,如下图所示:
![]()
那么Meta Learning的定义就可以表述为:根据资料找一个找一个函数f的函数 F 的能力,如下图所示:

现在,清楚了Meta Learning的架构搭建思路以后,我们就可以顺着该思路一步一步寻找解决方案。
首先第一步要做的,是准备Meta
Learning的训练资料。前面说过,Meta Learning的训练资料是一堆![]() 和一堆
和一堆![]() 的组合,显然一堆
的组合,显然一堆![]() 是很好准备的,于是重点在于,一堆
是很好准备的,于是重点在于,一堆![]() 该如何准备。事实上,
该如何准备。事实上,![]() 本身是一个抽象概念,我们需要知道它的具体实例是什么,不妨以传统的神经网络为例来介绍。
本身是一个抽象概念,我们需要知道它的具体实例是什么,不妨以传统的神经网络为例来介绍。
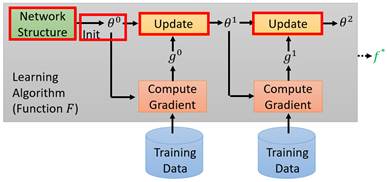
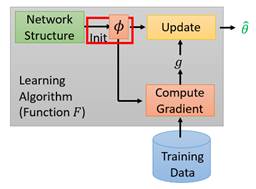
上图是大家都熟悉的梯度下降算法,它的流程可以简述为:设计一个网络架构->给参数初始化->读入训练数据批次->计算梯度->基于梯度更新参数->进入下一轮训练->……。对于每一个具体的任务来说,它的全部算法流程就构成了一个![]() ,也就是说,(如图中红色框架)每当我们采用了一个不同的网络架构,或使用了不同的参数初始化,或决定了不同的参数更新方式时,我们都在定义一个新的
,也就是说,(如图中红色框架)每当我们采用了一个不同的网络架构,或使用了不同的参数初始化,或决定了不同的参数更新方式时,我们都在定义一个新的![]() 。所以,针对梯度下降算法来说,Meta Learning的最终学习成果是在给定训练资料的条件下,机器能够找到针对这笔资料的SGD最佳训练流程(
。所以,针对梯度下降算法来说,Meta Learning的最终学习成果是在给定训练资料的条件下,机器能够找到针对这笔资料的SGD最佳训练流程(![]() )。因此,前边我们探讨的为Meta Learning准备的
)。因此,前边我们探讨的为Meta Learning准备的![]() ,实际上是由包含尽量多和丰富的组合方式的不同训练流程来组成的。
,实际上是由包含尽量多和丰富的组合方式的不同训练流程来组成的。
接下来,第二步要做的,就是设计评价函数 F好坏的指标。具体来说,F可以选择各种不同的训练流程![]() ,如何评价F找到的现有流程
,如何评价F找到的现有流程![]() ,以及如何提升
,以及如何提升![]() ,这是Meta Learning中比较重要的部分。
,这是Meta Learning中比较重要的部分。
我们先来说明Meta Learning中函数F的损失函数的定义。
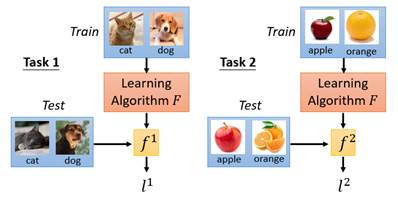
如上图所示,在Task1中,函数F学习到的训练算法是![]() ,而Task1中的测试集在
,而Task1中的测试集在![]() 上的测试结果被记作在Task1上的损失值
上的测试结果被记作在Task1上的损失值![]() (注意测试结果不仅仅可以是分类任务中的分类损失,也可以定义为损失下降的速率等等,取决于我们希望F学习到什么样的算法效果);同理,在Task2中的测试集在
(注意测试结果不仅仅可以是分类任务中的分类损失,也可以定义为损失下降的速率等等,取决于我们希望F学习到什么样的算法效果);同理,在Task2中的测试集在![]() 上的测试结果记作在Task2上的损失值
上的测试结果记作在Task2上的损失值![]() 。最终,函数F的损失函数就定义为所有Task上的损失的总和:
。最终,函数F的损失函数就定义为所有Task上的损失的总和:
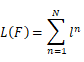
损失函数定义完毕后,我们该如何降低F的损失呢?由于Meta Learning的求解是非常复杂的过程,我们先以MAML算法为例讲解一个Meta Learning的简单情况的求解。
第三章 Meta Learning的简单实例:MAML
MAML算法想要解决的问题是,对于F在每一个任务中学习到的![]() ,规定
,规定![]() 只负责决定参数的赋值方式,而不设计模型的架构,也不改变参数更新的方式。也就是说,MAML中的
只负责决定参数的赋值方式,而不设计模型的架构,也不改变参数更新的方式。也就是说,MAML中的![]() 的网络结构和更新方式都是提前固定的,MAML要解决的是如何针对不同任务为网络赋不同的初始值。
的网络结构和更新方式都是提前固定的,MAML要解决的是如何针对不同任务为网络赋不同的初始值。
如上图所示,![]() 只需考虑参数的初始化方式。假设当前参数的初始化为
只需考虑参数的初始化方式。假设当前参数的初始化为![]() ,将
,将![]() 应用于所有的训练任务中,并将所有任务最终训练结束后的参数记作
应用于所有的训练任务中,并将所有任务最终训练结束后的参数记作![]() (
(![]() 表示第
表示第![]() 个任务),然后该参数下的测试损失记作
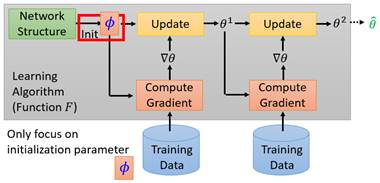
个任务),然后该参数下的测试损失记作![]() 。于是,当前的初始化参数
。于是,当前的初始化参数![]() 的损失函数就表示为:
的损失函数就表示为:
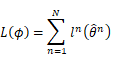
接下来,我们需要求解![]() ,使得:
,使得:
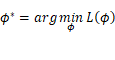
将![]() 放入梯度下降算法中,得到:
放入梯度下降算法中,得到:
![]()
MAML为了更快地计算出上式的结果,做了两处计算上的调整。
首先,如上图所示,由于在每一个训练任务上更新多次参数会占用太多时间,因此MAML选择只更新一次的参数结果作为该任务下的最终参数![]() ,即只走一次梯度下降:
,即只走一次梯度下降:
![]()
能这样做的原因是,如果模型只需训练一次就能达到好的效果,那么这样的训练初始参数基本上能符合好的参数,不过,在测试资料上依然需要训练多次以检验该初始参数的真正效果。
MAML的第二处调整是,对于![]() 的实际计算做了简化。由于
的实际计算做了简化。由于

不妨观察一下![]() 的展开式:
的展开式:
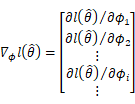
而![]() 与
与![]() 的具体关系是:
的具体关系是:
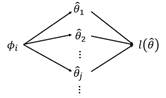
由此可以得到![]() 的具体计算式为:
的具体计算式为:
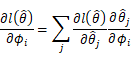
很明显,上式的第一项![]() 是容易计算的,因为它直接取决于
是容易计算的,因为它直接取决于![]() 函数的定义是什么,下面我们来求解第二项
函数的定义是什么,下面我们来求解第二项![]() 。
。
将![]() 带回到
带回到![]() 中,得到:
中,得到:
![]()
注意到当![]() 时,有:
时,有:
![]()
当![]() 时,有:
时,有:
![]()
现在的问题是,由于上式含有二次微分,并不好计算,MAML提出将二次微分项(![]() )直接舍弃掉(这种仅保留一次微分项的方法叫做“first-order approximation”)。
)直接舍弃掉(这种仅保留一次微分项的方法叫做“first-order approximation”)。
舍弃二次微分项之后的计算结果就变成了:
![]()
带回到![]() 的计算式中,得到:
的计算式中,得到:
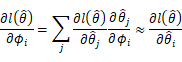
进而得到最开始![]() 的展开式变为:
的展开式变为:
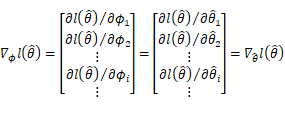
综上,简化后的MAML计算就变得简单许多,MAML的理论分析也到此结束。下面我们用一个实际的例子来理解上面的计算是如何执行的。
![]()
首先,最开始有一个初始化的参数![]() 。
。

然后,在Task m上训练一次![]() 得到最终参数
得到最终参数![]() ,接着计算
,接着计算![]() 的梯度(即上图中第二根绿色箭头),将这一梯度乘以学习率赋给
的梯度(即上图中第二根绿色箭头),将这一梯度乘以学习率赋给![]() ,得到
,得到![]() 的第一次更新结果
的第一次更新结果![]() 。
。
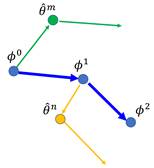
接下来,同样地,在Task n上训练一次![]() 得到最终参数
得到最终参数![]() ,接着计算
,接着计算![]() 的梯度(即上图中第二根黄色箭头),将这一梯度乘以学习率赋给
的梯度(即上图中第二根黄色箭头),将这一梯度乘以学习率赋给![]() ,得到第二次训练的更新结果
,得到第二次训练的更新结果![]() 。
。
这样不断循环往复,直至在所有的训练Task上完成训练,就找到了最终的初始化参数![]() 。
。
上述就是MAML算法的完整介绍,其实参数初始化问题还有很多其他的解法,其中一个有趣的想法是用LSTM来训练![]() ,因为梯度下降算法本质上可以看作序列模型(如下图所示),于是通过改LSTM的架构也能实现
,因为梯度下降算法本质上可以看作序列模型(如下图所示),于是通过改LSTM的架构也能实现![]() 的训练:
的训练:
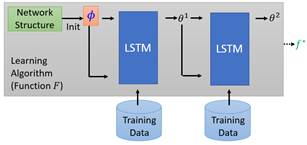
具体的实现过程就不在此细述了,感兴趣的读者可以去观看李宏毅老师的视频教程:
https://www.bilibili.com/video/av46561029/?p=41
第四章 Meta Learning的复杂问题的解决方案
上篇介绍的MAML,只是解决了Meta Learning中一个较为简单的问题:如何为模型赋值初始化参数。Meta Learning中还有很多更复杂的问题,譬如如何设计模型的架构,以及如何构造参数更新的方式等。由于这些问题涉及到的![]() 的求解已经不可微分,因此无法用梯度下降算法进行求解,我们只能考虑使用强化学习(Reinforcement Learning)。
的求解已经不可微分,因此无法用梯度下降算法进行求解,我们只能考虑使用强化学习(Reinforcement Learning)。
4.1.Meta Learning如何设计模型架构
先考虑第一个问题:如何设计一个能够设计模型的模型?假设我们的任务是学习设计CNN模型,可以考虑引入RNN网络来实现设计CNN。

如上图所示,RNN横向的宽度取决于待设计网络的层数,而纵向的每一个cell的输出就对应网络的具体单元配置。譬如在设计CNN的网络中,RNN会输出一系列数据,分别对应到每个卷积核的具体参数配置,例如卷积核数目、核高度、核宽度、步幅高度、步幅宽度等。值得注意的是,每决定一个参数后,该参数就会成为下一个参数的输入,所以第一层的参数设计至关重要,它会影响到接下来的所有设计。
设计完网络之后,我们需要评价此网络的好坏。首先依据给出的参数搭建好对应的网络,然后将该网络应用于众多训练Task中进行训练,并在训练完成后计算准确性(Accuracy)。值得注意的是,由于无法进行梯度下降,该准确性只能作为reward反馈给设计网络,并用强化学习的方式让网络在大量reward下学会产生更好的网络。
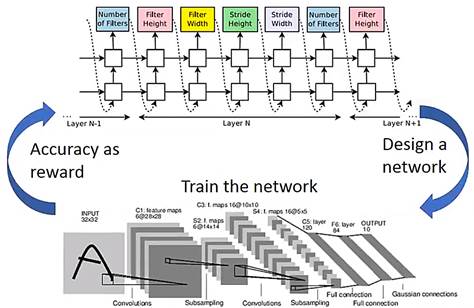
上述的训练方式有一个显著的弊端是,得到大量reward消耗的时间是非常久的,譬如在谷歌一篇设计LSTM网络架构的文献中的方法,需要同时用450块GPU跑3-4天。我们可以用weight share的方法来降低得到reward的时间,简单来说,就是对于采用过的模块设计,直接将上一次采用该模块时训练得到的参数复制过来,作为该模块的初始化参数,这样能大幅加快新网络的训练收敛时间。实验证明,该方法让谷歌提出的设计LSTM架构的网络的训练时间,缩短到在1080Ti上仅需16小时。
下面展示一个用meta learning设计出的LSTM架构(如下右图):
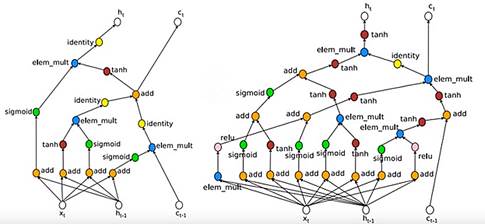
可以看出,右边机器设计的LSTM比左边人工设计的LSTM要复杂许多,其中一个有意思的地方是,右边机器设计的LSTM中完全没有使用sin函数,这与人的设计方式是一致的。而最终实验结果证明,右边的LSTM的训练效果,比左边的LSTM有少量提升。
4.2.Meta Learning如何设计参数更新策略
这一节来介绍如何设计新的参数更新策略的网络。实际上,每一个参数更新策略,都可以看作由一个五元组构成。
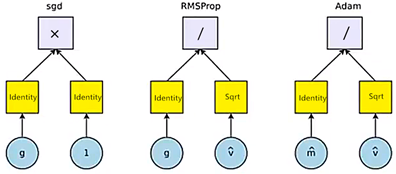
如上图所示,列举了三个最熟知的参数更新算法:SGD、RMSProp和Adam。每个5元组中左下角蓝色区域代表第一个操作数(记作![]() ,通常指梯度),右下角蓝色区域代表第二个操作数(记作
,通常指梯度),右下角蓝色区域代表第二个操作数(记作![]() ,通常指学习率),左边黄色区域代表
,通常指学习率),左边黄色区域代表![]() 的单元计算(
的单元计算(![]() ),右边黄色区域代表
),右边黄色区域代表![]() 的单元计算(
的单元计算(![]() ),最上边紫色区域代表对两个单元计算结果的二元计算(
),最上边紫色区域代表对两个单元计算结果的二元计算(![]() )。
)。
不妨将上图中的表达式代入三个参数更新算法中,得到SGD的更新值![]() ,RMSProp的更新值
,RMSProp的更新值![]() ,以及Adam的更新值:
,以及Adam的更新值:![]() 。因此,如过想设计新的参数更新算法,我们可以使用如下的RNN网络:
。因此,如过想设计新的参数更新算法,我们可以使用如下的RNN网络:
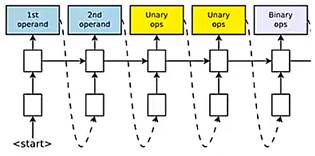
这个网络很好理解,每个cell输出对应元件的选择项,最后组合在一起就是新设计的参数更新算法。其中各个元件的可选项有:

下面展示一个用meta learning设计出的更新策略——PowerSign。
![]()
如上式所示,其中![]() 代表
代表![]() ,
,![]() 代表
代表![]() ,
,![]() 取决于
取决于![]() 与
与![]() 是否同向,若同向它的值就大一些,若不同向它的值就小一些。下面看一下PowerSign的实验结果:
是否同向,若同向它的值就大一些,若不同向它的值就小一些。下面看一下PowerSign的实验结果:
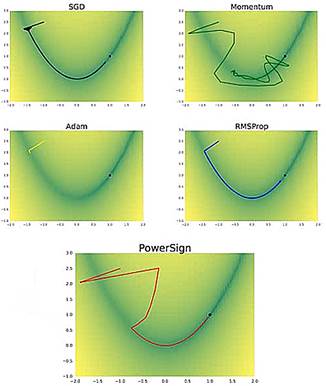
可以看出,在月牙型的梯度训练轨迹下,SGD、Adam和RMSProp都无法走到终点,Momentum能到达终点但非常慢,只有PowerSign能较快地到达终点。由此可以看出,由meta learning设计的参数更新策略在某些情况下是占有优势的。
4.3.Meta Learning如何设计激活函数
激活函数同样遵循如下的设计范式(即激活函数仅对x操作,一般不超过两次计算):
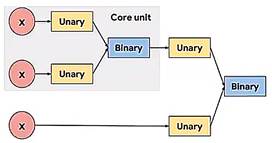
依据这一范式可以构造出对应的设计网络:
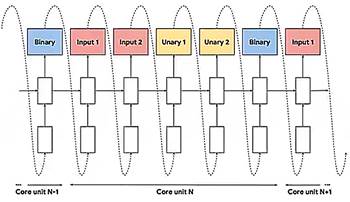
其中各个元件的可选项有:
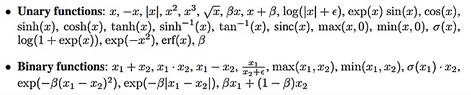
下面展示一个用meta learning设计出的激活函数——Swish。
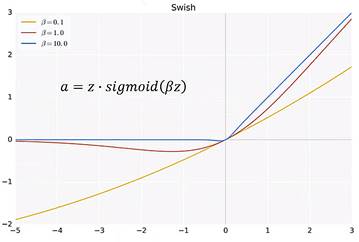
如上图所示,当取β=1.0的时候Swish的实验效果是最好的。有意思的地方在于,Swish(β=1.0)的形状有点像Relu和Leaky Relu的结合,因为在从0向负走的时候,Swish是先降低后又回归接近于0。下面我们看一下Swish的实验测试结果:

可以看出,Swish对于所有基线的比较都是占优的,特别是在与Relu的比较中,在9个任务集上达到了完胜。
综上,关于meta learning在复杂网络设计上的方法已全部介绍完毕。上述的这些网络设计模块还能通过组合使用,从而设计出包含模型架构、激活函数和更新策略在内的更复杂、更完善的网络。
第五章 Meta Learning的未来趋势
总的来说,meta learning还是一个挺神奇的研究方向,而且它解决的问题也颇具实际意义。除了前边介绍的诸多meta learning方法之外,还有一些奇妙的领域有待人们研究和开拓,下边将介绍Learn to Learn to Learn问题和F函数黑盒化想法。
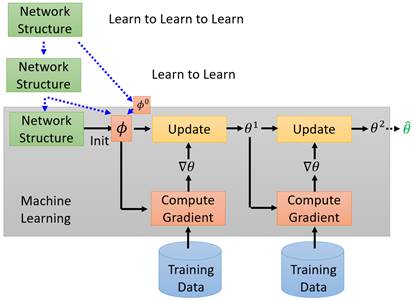
首先Learn to
Learn to Learn问题解决的是,如何学习一个模型,它能够学习出会学习的模型。举一个实例来说,在第三节中介绍的MAML,能够学习为模型初始化参数![]() ,那么这个参数
,那么这个参数![]() 本身的初始化
本身的初始化![]() (也就是初始化参数的初始化参数),依然是一个可以被学习的内容(如上图所示);再比如,4.1节中介绍的RNN模型,能够设计出CNN模型,而这个RNN模型本身的设计,也可以被一个能设计模型的模型来学习(如上图所示)……循环往复,我们可以衍生出一系列Learn to Learn to Learn,甚至是Learn to N Learn问题。而解决这些问题对于Meta Learning来说是具有里程碑意义的,因为那标志着机器学习的完全自动化。
(也就是初始化参数的初始化参数),依然是一个可以被学习的内容(如上图所示);再比如,4.1节中介绍的RNN模型,能够设计出CNN模型,而这个RNN模型本身的设计,也可以被一个能设计模型的模型来学习(如上图所示)……循环往复,我们可以衍生出一系列Learn to Learn to Learn,甚至是Learn to N Learn问题。而解决这些问题对于Meta Learning来说是具有里程碑意义的,因为那标志着机器学习的完全自动化。

另外一个值得研究的领域是F函数的黑盒化想法。因为,当前F学到的策略![]() 是透明的,并且人为限制了策略
是透明的,并且人为限制了策略![]() 的内容,所以其结果不一定是机器学习能产生的最优结果。如果我们减少人为的影响,将F和
的内容,所以其结果不一定是机器学习能产生的最优结果。如果我们减少人为的影响,将F和![]() 封装成一个更大的目标H,让机器自己去学习F和
封装成一个更大的目标H,让机器自己去学习F和![]() 的关系,其中H的输入是训练资料+测试资料,输出是测试资料的预测结果,或许能让机器学习到更好的结果。
的关系,其中H的输入是训练资料+测试资料,输出是测试资料的预测结果,或许能让机器学习到更好的结果。
这方面已经有一些应用在尝试,譬如人脸辨识领域——输入一堆人脸库和一张测试人脸,输出预测该人脸是否是人脸库中的人脸。具体的做法及相关研究在此不再细述,感兴趣的读者可以观看李宏毅老师的视频教程:
https://www.bilibili.com/video/av46561029/?p=44
综上,Meta Learning的介绍到此就结束了,下一篇将回归到GANs上,介绍Meta Learning与GANs的结合,并且讲述它们在少样本学习上取得的成果和应用。
评 论
